Question

The total amount spent by some number of people on clothing and footwear in the years​ 2000-2009 can be modeled by the quadratic function ​f(x)=-4.122x^2+72.01x+97.21​, where x=0 represents January​ 1, 2000, x=1 represents January​ 1, 2001, and so​ on, and​ f(x) is in billions of dollars. According to the​ model, in what year during this period was the amount spent on clothing and footwear a​ maximum?

Answer 1

The maximum amount spent on clothing and footwear occured in late 2008.

Explanation:

The existence of a maximum in a continuous differentiable function is determined by the First and Second Derivative Test, which consist on the following process:

1) First and second derivatives of the given function are obtained.

2) First derivative is equalized to zero and roots are found. (Critical points)

3) Each critical point is evaluated in the second derivative expression in order to determine if each point is an absolute maximum (f'' < 0) or minimum (f'' > 0).

The first and second derivatives of the function are, respectively:

`f'(x) = -8.244\cdot x + 72.01`

`f''(x) = -8.244`

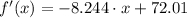
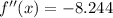
Since first derivative is a first-order polynomial (linear function), there is a root, which is found herein:

`-8.244\cdot x +72.01 = 0`

`x = 8.734`

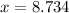
The second derivative indicates that critical value leads to an absolute maximum, therefore, the maximum amount spent on clothing and footwear occured in late 2008.