Question

>>>>>>>>> Use graphs and tables to find the limit and identify any vertical asymptotes of the function. limit of 1 divided by the quantity x minus 10 as x approaches 10 from the left

Answer 1

`\displaystyle \lim_(x \to 10^-) (1)/(x - 10) = -\infty`

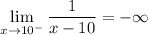
General Formulas and Concepts:

Calculus

Limits

• Right-Side Limit:
  `\displaystyle \lim_(x \to c^+) f(x)`
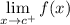
• Left-Side Limit:
  `\displaystyle \lim_(x \to c^-) f(x)`

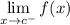
Graphical Limits

Explanation:

If we graph the function, we can see that as we approach 3 from the left, we go towards negative infinity.

∴
`\displaystyle \lim_(x \to 10^-) (1)/(x - 10) = -\infty`

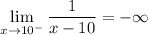
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits