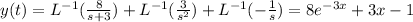Question

Consider the initial value problem y' + 3y = 9t, y(0) = 7.

a. Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y(s). Do not move any terms from one side of the equation to the other (until you get to part (b) below).
b. Solve your equation for Y(s).
Y(s) = L {y(t)} =
c. Take the inverse Laplace transform of both sides of the previous equation to solve for y(t).
y(t) =

Answer 1

`y(t) = 3x+8e^(-3x) -1`

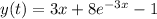
Explanation:

Recall that the following laplace transforms

`L(y') = sY(s)-y(0)`

`L(t) = (1)/(s^2)`

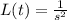
The laplace transform is linear, so, applying the laplace transform to the equation we get

`L(y'+3y) = sY(s)-7+3Y(s) = L(9t) = (9)/(s^2)`

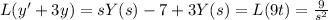
By some algebraic manipulations, we get

`Y(s)(s+3) = (9+7s^2)/(s^2)`

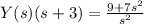
which is equivalent to

`Y(s) = (9+7s^2)/(s^2(s+3)) = (9)/(s^2(s+3))+(7)/(s+3)`

By using the partial fraction decomposition, we get

`(9)/(s^2(s+3)) = (-1)/(s) + (3)/(s^2) + (1)/(s+3)`

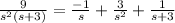
then

`Y(s) = (-1)/(s) + (3)/(s^2) + (1)/(s+3) + (7)/(s+3) = (8)/(s+3) + (3)/(s^2)-(1)/(s)`

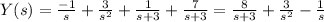
Using that

`L(e^(-ax)) = (1)/(s+a)`

`L(1) = (1)/(s)`

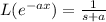
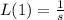
by taking the inverse on both sides we get

`y(t) = L^(-1)((8)/(s+3))+L^(-1)((3)/(s^2))+L^(-1)(-(1)/(s)) = 8e^(-3x) + 3x-1`