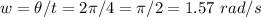Answer:
A. b) Directed towards center
B.
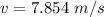
C.
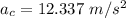
D.

Step-by-step explanation:
The "force" that they feel pressing their backs against the wall is because the reaction to the centripetal acceleration .
A.
This acceleration has its direction towards the center of the circle. (option b)
B.
Their linear speed can be calculated with the equation:
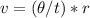
Where
 is the total angular position moved in radians (
is the total angular position moved in radians (
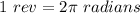 ), 't' is the time elapsed for the angular position moved and 'r' is the radius. So we have that:
), 't' is the time elapsed for the angular position moved and 'r' is the radius. So we have that:
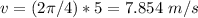
C.
The centripetal acceleration is given by the equation:

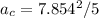
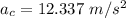
D.
Their angular speed is given by the equation: