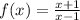Answer:
Answer C:
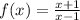
Explanation:
Notice that all the functions look like x plus a constant in the numerator, and x minus the same constant in the denominator.
So we can do a general analysis finding the inverse of a function of the form:
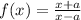
and finding which value of "a" will make
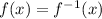
To find the inverse we need to solve for "x" in the equivalent equation:
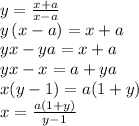
Then, we see that if
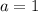 , then the expression for
, then the expression for
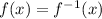
Then the function that verifies this condition is: