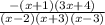Answer:
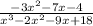
Explanation:
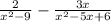
Factor x²-9 and x²-5x+6.

Least common multiple of (x+3), (x-3), (x-2), and (x-3) is (x+3), (x-3), and (x-2).
Adjust the fractions based on LCM.

Subtract the fractions since denominators are equal.
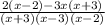
Expand.
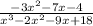
The fraction can be in factored form.