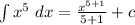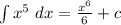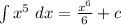Answer:
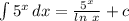
Explanation:
Note that the integral of
 is not
is not
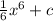
The solution is as follows:
Given

Required
Integrate
Represent the given expression using integral notation
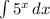
This question can't be solved directly;
We'll make use of exponential rules which states;
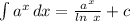
By comparing
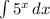 with
with
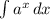 ;
;
we can substitute 5 for a;
Hence, the expression
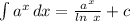 becomes
becomes
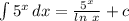
-------------------------------------------------------------------------------------
However, the integral of
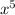 is
is
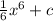
This is shown below:
Given that
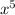
Applying power rule;
Power rule states that

In this case (
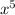 ), n = 5;
), n = 5;
So,
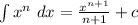
becomes