Question

An incomplete distribution is given below:Variable You are given that the median value is 70 and the total number of items is 200. Using the median formula fill up the frequencies.

Answer 1

The missing frequencies are x = 8 and y = 43.

Explanation:

Median Value =70

Then the median Class =60-80

Let the missing frequencies be x and y.

Given: Total Frequncy = 200 , Median = 46

From the table

`\sum f_i =149+x+y`

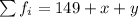
Here, n = 200

n/2 = 100

Lower Class Boundary of the median class, l=60

Frequency of the median class(f) =66

Cumulative Frequency before the median class, f=42+x

Class Width, h=10

`Median = l + ((n)/(2) - c.f )/(f) * h`

`70 = 60+ (100- 42+x )/(66)* 10\\70 = 60+ (58+x )/(66)* 10\\70-60=(58+x )/(66)* 10\\10*66=10(58+x)\\58+x=66\\x=66-58\\x=8`

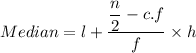
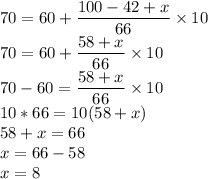
200=149+x+y

200=149+8+y

y=200-(149+8)

y=43

Hence, the missing frequencies are x = 8 and y = 43.