Answer:
The missing frequencies are x = 8 and y = 43.
Explanation:
Median Value =70
Then the median Class =60-80
Let the missing frequencies be x and y.
Given: Total Frequncy = 200 , Median = 46
![\left|\begin{array}cccccccValue&0-20&20-40&40-60&60-80&80-100&100-120&120-140\\Frequency&12&30&x&66&y&27&14\\$Cumu.Freq&12&42&42+x&108+x&108+x+y&135+x+y&149+x+y\end{array}\right|]()
From the table
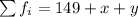
Here, n = 200
n/2 = 100
Lower Class Boundary of the median class, l=60
Frequency of the median class(f) =66
Cumulative Frequency before the median class, f=42+x
Class Width, h=10
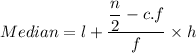
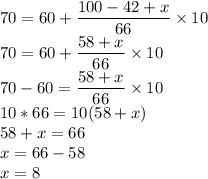
200=149+x+y
200=149+8+y
y=200-(149+8)
y=43
Hence, the missing frequencies are x = 8 and y = 43.