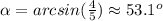Answer:
a)
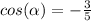
b)
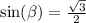
c)
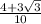
d)
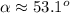
Explanation:
a) The problem tells us that angle
 is in the second quadrant. We know that in that quadrant the cosine is negative.
is in the second quadrant. We know that in that quadrant the cosine is negative.
We can use the Pythagorean identity:
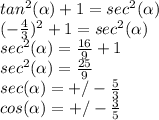
Where we have used that the secant of an angle is the reciprocal of the cos of the angle.
Since we know that the cosine must be negative because the angle is in the second quadrant, then we take the negative answer:
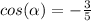
b) This angle is in the first quadrant (where the sine function is positive. They give us the value of the cosine of the angle, so we can use the Pythagorean identity to find the value of the sine of that angle:
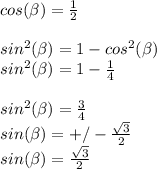
where we took the positive value, since we know that the angle is in the first quadrant.
c) We can now find
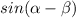 by using the identity:
by using the identity:
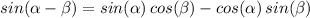
Notice that we need to find
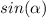 , which we do via the Pythagorean identity and knowing the value of the cosine found in part a) above:
, which we do via the Pythagorean identity and knowing the value of the cosine found in part a) above:
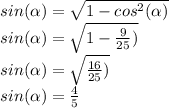
Then:
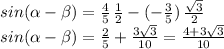
d)
Since
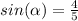
then