Question

Poly(3-hydroxybutyrate) (PHB), a semicrystalline polymer that is fully biodegradable and biocompatible, is obtained from renewable resources. From a sustain-ability perspective, PHB offers many attractive proper-ties though it is more expensive to produce than standard plastics. The accompanying data on melting point (°C) for each of 12 specimens of the polymer using a differential scanning calorimeter appeared in the article "The Melting Behaviour of Poly(3-1-1ydroxybutyrate) by DSC. Reproducibility Study" (Polymer Testing, 2013: 215-220).

180.5 181.7 180.9 181.6 182.6 181.6

181.3 182.1 182.1 180.3 181.7 180.5

Compute the following:

a. The sample range

b. The sample variance S2 from the definition (Hint: First subtract 180 from each observation.]

c. The sample standard deviation

d. S2 using the shortcut method

Answer 1

(a) 2.3

(b) 0.5245

(c) 0.7242

(d) 0.5245

Explanation:

The data provided is:

S = {180.5, 181.7, 180.9, 181.6, 182.6, 181.6, 181.3, 182.1, 182.1, 180.3, 181.7, 180.5}

(a)

The formula to compute the sample range is:

`\text{Sample Range}=\text{max.}_(x)-\text{min.}_(x)`

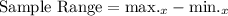
The data set arranged in ascending order is:

S' = {180.3 , 180.5 , 180.5 , 180.9 , 181.3 , 181.6 , 181.6 , 181.7 , 181.7 ,, 182.1 , 182.1 , 182.6}

The minimum value is, 180.3 and the maximum value is, 182.6.

Compute the sample range as follows:

`\text{Sample Range}=\text{max.}_(x)-\text{min.}_(x)`

`=182.6-180.3\\=2.3`

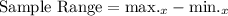
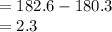
Thus, the sample range is 2.3.

(b)

Compute the sample variance as follows:

`S^(2)=(1)/(n-1)\sum(x_(i)-\bar x)^(2)`

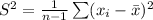
`=(1)/(12-1)* [(180.5-181.41)^(2)+(181.7-181.41)^(2)+...+(180.5-181.41)^(2)]\\\\=(1)/(11)* 5.7692\\\\=0.524473\\\\\approx 0.5245`

Thus, the sample variance is 0.5245.

(c)

Compute the sample standard deviation as follows:

`s=\sqrt{S^(2)}`

`=√(0.5245)\\\\=0.7242`

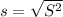
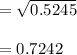
Thus, the sample standard deviation is 0.7242.

(d)

Compute the sample variance using the shortcut method as follows:

`S^(2)=(1)/(n-1)\cdot [\sum x_(i)^(2)-n(\bar x)^(2)]`

`=(1)/(12-1)\cdot [394913.57-(12* (181.41)^(2)]\\\\=(1)/(11)* [394913.57-394907.80]\\\\=(5.77)/(11)\\\\=0.5245`

Thus, the sample variance is 0.5245.