Answer:
Step-by-step explanation:
Maximum occurs when the path difference is an integral multiple of wavelength
Here
 - Wavelength,
- Wavelength,
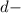 slit separation and
slit separation and
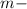 Order of pattern
Order of pattern
Rearrange the equation for
![\begin{aligned}d &=(m \lambda)/(\sin \theta) \\</p><p>\text { Here, } \sin \theta &=(y)/(L) \quad\left(\begin{array}{l}</p><p>\text { Here, } L-\text { separation between slit and screen } \\</p><p>y-\text { Distance between respective fringe from center on screen }\end{array}\right)]()
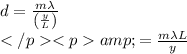
Here, order
Due to the fact that there are 11 bright fringes seen, you take
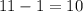
since starts from 0,1,2,3
Substitute given values
