Question

A 0.3-m-radius automobile tire rotates how many revolutions after starting from rest and accelerating at a constant 2.13 rad/s2 over a 23.2-s interval?

Answer 1

The automobile tire rotates 91 revolutions

Step-by-step explanation:

Given;

angular acceleration of the automobile, α = 2.13 rad/s²

time interval, t = 23.2-s

To calculate the number of revolutions, we apply the first kinematic equation;

`\theta = \omega_i \ + (1)/(2) \alpha t^2`

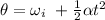
the initial angular velocity is zero,

`\theta =0\ + (1)/(2) (2.13) (23.2)^2\\\\\theta = 573.2256 \ Rad`

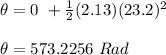
Find how many revolutions that are in 573.2256 Rad

`N = (\theta)/(2 \pi) = (573.2256)/(2\pi) \\\\N = 91 \ revolutions`

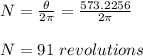
Therefore, the automobile tire rotates 91 revolutions