Answer:
The speed of the arrow after passing through the target is 30.1 meters per second.
Step-by-step explanation:
The situation can be modelled by means of the Principle of Linear Momentum, let suppose that the arrow and the target are moving on the same axis, where the velocity of the first one is parallel to the velocity of the second one. The Linear Momentum model is presented below:
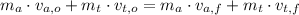
Where:
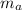 ,
,
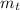 - Masses of arrow and target, measured in kilograms.
- Masses of arrow and target, measured in kilograms.
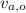 ,
,
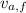 - Initial and final speeds of the arrow, measured in meters per second.
- Initial and final speeds of the arrow, measured in meters per second.
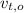 ,
,
 - Initial and final speeds of the target, measured in meters per second.
- Initial and final speeds of the target, measured in meters per second.
The final speed of the arrow is now cleared:

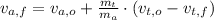
If
 ,
,
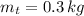 ,
,
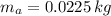 ,
,
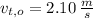 and
and
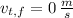 , the speed of the arrow after passing through the target is:
, the speed of the arrow after passing through the target is:
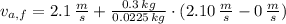
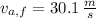
The speed of the arrow after passing through the target is 30.1 meters per second.