Question

Suppose you take a 30-question, multiple-choice test, in which each question contains 4 choices: A, B, C, and D. If you randomly guess on all 30 questions, what is the probability you pass the exam (correctly guess on 60% or more of the questions)? Assume none of the questions have more than one correct answer (hint: this assumption of only 1 correct choice out of 4 makes the distribution of X, the number of correct guesses, binomial). What is the expected number of correct guesses, from problem #19? What is the standard deviation, ? (Remember that X is a binomial random variable!) What would be considered an unusual number of correct guesses on the test mention in problem number 19 using ?

Answer 1

(a) The probability you pass the exam is 0.0000501.

(b) The expected number of correct guesses is 7.5.

(c) The standard deviation is 2.372.

Explanation:

We are given that you take a 30-question, multiple-choice test, in which each question contains 4 choices: A, B, C, and D. And you randomly guess on all 30 questions.

Since there is an assumption of only 1 correct choice out of 4 which means the above situation can be represented through binomial distribution;

`P(X =x) = \binom{n}{r}* p^(r)* (1-p)^(n-r) ; x = 0,1,2,3,......`

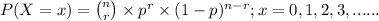
where, n = number of trials (samples) taken = 30

r = number of success = at least 60%

p = probbaility of success which in our question is the probability

of a correct answer, i.e; p =
`(1)/(4)` = 0.25

Let X = Number of questions that are correct

So, X ~ Binom(n = 30 , p = 0.25)

(a) The probability you pass the exam is given by = P(X
`\geq` 18)

Because 60% of 30 = 18

P(X
`\geq` 18) = P(X = 18) + P(X = 19) +...........+ P(X = 29) + P(X = 30)

=
`\binom{30}{18}* 0.25^(18)* (1-0.25)^(30-18) + \binom{30}{19}* 0.25^(19)* (1-0.25)^(30-19) +.......+ \binom{30}{29}* 0.25^(29)* (1-0.25)^(30-29) + \binom{30}{30}* 0.25^(30)* (1-0.25)^(30-30)`

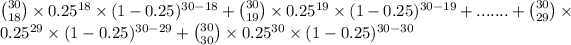
= 0.0000501

(b) The expected number of correct guesses is given by;

Mean of the binomial distribution, E(X) =
`n * p`

=
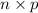
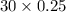`30 * 0.25` = 7.5

(c) The standard deviation of the binomial distribution is given by;

S.D.(X) =
`√(n * p * (1-p))`

=
`√(30 * 0.25 * (1-0.25))`

=
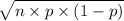
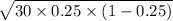
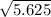`√(5.625)` = 2.372