Answer:
(a) The probability you pass the exam is 0.0000501.
(b) The expected number of correct guesses is 7.5.
(c) The standard deviation is 2.372.
Explanation:
We are given that you take a 30-question, multiple-choice test, in which each question contains 4 choices: A, B, C, and D. And you randomly guess on all 30 questions.
Since there is an assumption of only 1 correct choice out of 4 which means the above situation can be represented through binomial distribution;
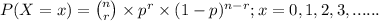
where, n = number of trials (samples) taken = 30
r = number of success = at least 60%
p = probbaility of success which in our question is the probability
of a correct answer, i.e; p =
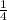 = 0.25
= 0.25
Let X = Number of questions that are correct
So, X ~ Binom(n = 30 , p = 0.25)
(a) The probability you pass the exam is given by = P(X
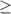 18)
18)
Because 60% of 30 = 18
P(X
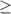 18) = P(X = 18) + P(X = 19) +...........+ P(X = 29) + P(X = 30)
18) = P(X = 18) + P(X = 19) +...........+ P(X = 29) + P(X = 30)
=
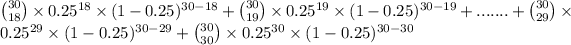
= 0.0000501
(b) The expected number of correct guesses is given by;
Mean of the binomial distribution, E(X) =
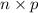
=
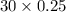 = 7.5
= 7.5
(c) The standard deviation of the binomial distribution is given by;
S.D.(X) =
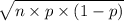
=
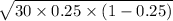
=
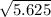 = 2.372
= 2.372