Answer:
4L
Step-by-step explanation:
Data provided in the question according to the question is as follows
Length = L
Gravity = G
For friend
Length = ?
Growth = 4G
Moreover,
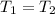
Based on the above information ,
Now we have to apply the simple pendulum formula which is shown below:
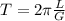
Now equates these equations in both sides
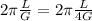
So after solving this, the length of the pendulum is 4L