Answer:
1st Harmonic:

3rd Harmonic:
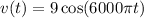
5th Harmonic:
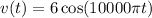
7th Harmonic:
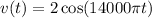
Step-by-step explanation:
The general form to represent a complex sinusoidal waveform is given by
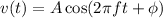
Where A is the amplitude in volts of the sinusoidal waveform
Where f is the frequency in cycles per second (Hz) of the sinusoidal waveform
Where
 is the phase angle in radians of the sinusoidal waveform.
is the phase angle in radians of the sinusoidal waveform.
1st Harmonic:
We have A = 50, f = 1000 and φ = 0

3rd Harmonic:
We have A = 9, f = 3000 and φ = 0
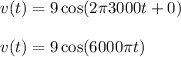
5th Harmonic:
We have A = 6, f = 5000 and φ = 0
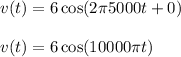
7th Harmonic:
We have A = 2, f = 7000 and φ = 0

Note: The even-numbered harmonics have 0 amplitude that is why they are not shown here.