Answer:
(a) The test statistic would follow a t distribution with n - 1 = 10 - 1 = 9 degrees of freedom.
(b) The test statistic is -2.2361.
(c) The p-value of the test is 0.026.
(d) α = 0.05.
Explanation:
In this case a hypothesis test is to be performed to determine whether the mean difference in the husband's versus the wife's satisfaction level is negative.
(a)
The data provided is paired data.
So a paired t-test would be used.
The test statistic would follow a t distribution with n - 1 = 10 - 1 = 9 degrees of freedom.
The hypothesis can be defined as follows:
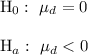
(b)
Compute the test statistic as follows:
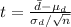

The test statistic is -2.2361.
(c)
Compute the p-value as follows:
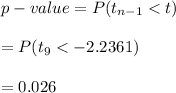
The p-value of the test is 0.026.
(d)
It is provided that the significance level of the test is, α = 0.05.