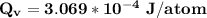Question

Calculate the energy (in J/atom) for vacancy formation in silver, given that the equilibrium number of vacancies at 800 C is 3.6 x 1017/cm3. The atomic weight and density for silver are 107.9 g/mol and 9.5 g/cm3, respectively

Answer 1

the energy vacancies for formation in silver is
`\mathbf{Q_v = 3.069*10^(-4) \ J/atom}`

Step-by-step explanation:

Given that:

the equilibrium number of vacancies at 800 °C

i.e T = 800°C is 3.6 x 10¹⁷ cm3

Atomic weight of sliver = 107.9 g/mol

Density of silver = 9.5 g/cm³

Let's first determine the number of atoms in silver

Let silver be represented by N

SO;

`N = (N_A* \rho _(Ag))/(A_(Ag))`

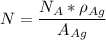
where ;

`N_A =` avogadro's number =
`6.023*10^(23) \ atoms/mol`

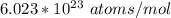
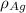`\rho _(Ag)` = Density of silver = 9.5 g/cm³

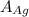`A_(Ag)` = Atomic weight of sliver = 107.9 g/mol

`N = ((6.023*10^(23) \ atoms/mol)*( 9.5 \ g/cm^3))/((107.9 \ g/mol))`

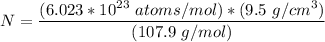
N = 5.30 × 10²⁸ atoms/m³

However;

The equation for equilibrium number of vacancies can be represented by the equation:

`N_v = N \ e^{^{-(Q_v)/(KT)}`

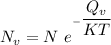
From above; Considering the natural logarithm on both sides; we have:

`In \ N_v =In N - (Q_v)/(KT)`

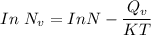
Making
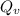`Q_v` the subject of the formula; we have:

`{Q_v = - {KT} In( ( \ N_v )/( N))`

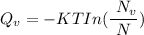
where;

K = Boltzmann constant = 8.62 × 10⁻⁵ eV/atom .K

Temperature T = 800 °C = (800+ 273) K = 1073 K

`Q _v =-( 8.62*10^(-5) \ eV/atom.K * 1073 \ K) \ In( (3.6*10^(17))/(5.3 0*10^(28)))`

`\mathbf{Q_v = 2.38 \ eV/atom}`

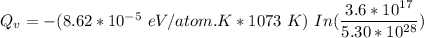
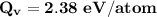
Where;

1 eV = 1.602176565 × 10⁻¹⁹ J

Then

`Q_v = (2.38 \ * 1.602176565 * 10^(-19) ) J/atom }`

`\mathbf{Q_v = 3.069*10^(-4) \ J/atom}`

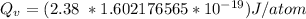
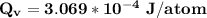
Thus, the energy vacancies for formation in silver is
`\mathbf{Q_v = 3.069*10^(-4) \ J/atom}`