Answer:
c = 0.1864
Explanation:
To find c, we need to find the z-score where:
P(-z<Z<z) = 98%
Based on the properties of the normal distribution we can said that
P(-z<Z<z) = 98% is equal to:
2*P(Z>z) = 2% or P(Z>z)= 1%
So, using the standard normal table, the z score is 2.33
Then, we can calculated the value of c as:
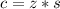
Where s is the standard deviation and z is the z-score. Replacing the values, we get:
c = 2.33*0.08
c = 0.1864