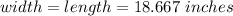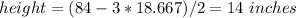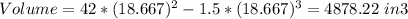Question

A country's postal service will accept a package if its length plus its girth (the distance all the way around) does not exceed 84 inches. Find the dimensions and volume of the largest package with a square base that can be mailed.

Answer 1

Dimensions: 18.667 x 18.667 x 14 inches

Volume: 4878.22 in3

Explanation:

If the length plus the girth does not exceed 84 inches, we have:

`length + (2*width+2*height) = 84`

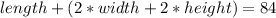
The box has a square base, to length = width, then we have:

`length + (2*length+2*height) = 84`

`3*length+2*height = 84`

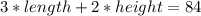
The volume of the box is given by the equation:

`Volume = length * width * height = length^2*height`

From the first equation, we have:

`height = (84 - 3*length)/2`

Using this height in the volume equation, we have:

`Volume = length^2*(84-3*length)/2`

`Volume = 42length^2-1.5*length^3`

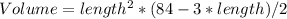
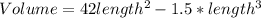
To find the maximum volume, we can find the value of length that makes the derivative of the volume in relation to the length equal zero:

`dV/dl = 84length - 4.5*length^2 = 0`

`84length = 4.5*length^2`

`length = 84/4.5 = 18.667\ inches`

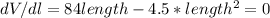
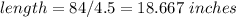
So the width, the height and the volume of the package are:

`width = length = 18.667\ inches`

`height = (84 - 3*18.667)/2 = 14\ inches`

`Volume = 42*(18.667)^2-1.5*(18.667)^3 = 4878.22\ in3`