Question

Prove that for all n E N\{0}, n3 + 2n and n4 +3n2 +1 are relatively prime.

Answer 1

Two expressions are relatively prime if their greatest common divisor is one.

Given the terms:
`n^3 + 2n$ and n^4 +3n^2 +1`,
`n \in N|\{0\}}`

`n^3 + 2n=n(n^2+2)\\n^4 +3n^2 +1$ is not factorizable\\`

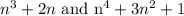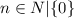
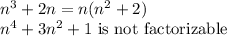
Therefore, the greatest common divisor of the two expressions is 1.

Therefore, for all n in the set of natural numbers, (where n cannot be zero.) The two expressions are relatively prime.