Answer:
Two expressions are relatively prime if their greatest common divisor is one.
Given the terms:
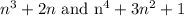 ,
,
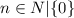
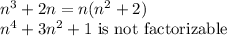
Therefore, the greatest common divisor of the two expressions is 1.
Therefore, for all n in the set of natural numbers, (where n cannot be zero.) The two expressions are relatively prime.