Question

Steam is contained in a closed rigid container which has a volume of 2 initially the the pressure and the temperature is the remeraturedrops as a result of heat transfer to the surroundings. Determine

a) the temperature at which condensation first occurs, in °C,
b) the fraction of the total mass that has condensed when the pressure reaches 0.5 bar.
c) What is the volume, in m3, occupied by saturated liquid at the final state?

Answer 1

The given question is incomplete. The complete question is as follows.

Steam is contained in a closed rigid container with a volume of 1 m3. Initially, the pressure and temperature of the steam are 10 bar and 500°C, respectively. The temperature drops as a result of heat transfer to the surroundings. Determine

(a) the temperature at which condensation first occurs, in
`^(o)C`,

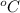(b) the fraction of the total mass that has condensed when the pressure reaches 0.5 bar.

(c) What is the volume, in
`m^(3)`, occupied by saturated liquid at the final state?

Step-by-step explanation:

Using the property tables

`T_(1) = 500^(o)C`,
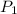`P_(1)` = 10 bar

`v_(1) = 0.354 m^(3)/kg`

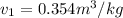
(a) During the process, specific volume remains constant.

`v_(g) = v_(1) = 0.354 m^(3)/kg`

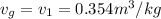
T =
`(150 - 160)^(o)C`

Using inter-polation we get,

T =
`154.71^(o)C`

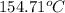
The temperature at which condensation first occurs is
`154.71^(o)C`.

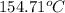(b) When the system will reach at state 3 according to the table at 0.5 bar then

`v_(f) = 1.030 * 10^(-3) m^(3)/kg`

`v_(g) = 3.24 m^(3) kg`

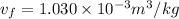
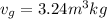
Let us assume "x" be the gravity if stream

`v_(1) = v_(f) + x_(3)(v_(g) - v_(f))`

`x_(3) = (v_(1) - v_(f))/(v_(g) - v_(f))`

=
`(0.3540 - 0.00103)/(3.240 - 0.00103)`

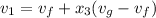
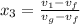
= 0.109

At state 3, the fraction of total mass condensed is as follows.

`(1 - x_(5))` = 1 - 0.109

= 0.891

The fraction of the total mass that has condensed when the pressure reaches 0.5 bar is 0.891.

(c) Hence, total mass of the system is calculated as follows.

m =
`(v)/(v_(1))`

=
`(1)/(0.354)`

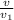
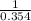
= 2.825 kg

Therefore, at final state the total volume occupied by saturated liquid is as follows.

`v_(ws) = m * v_(f)`

=
`2.825 * 0.00103`

=
`2.9 * 10^(-3) m^(3)`

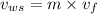
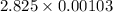
The volume occupied by saturated liquid at the final state is
`2.9 * 10^(-3) m^(3)`.