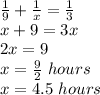Question

Working together to palms can drain a certain pool in three hours if it takes the older pump nine hours to drain the pool by itself how long will it take The newer pump to drain the pool on its own

Answer 1

It would take the newer pump 4.5 hours to drain the pool

Explanation:

Let's investigate first what is the fraction of the job done in the unit of time (hour in this case) by each pump if the work individually:

older pump: if it takes it 9 hours to complete the job, it does
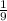`(1)/(9)` of the job in one hour.

newer pump: we don't know how long it takes (this is our unknown) so we call it "x hours". Therefore, in the unit of time (in one hour) it would have completed
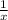`(1)/(x)` of the total job.

both pumps together: since it takes both 3 hours to complete the job, in one hour they do
`(1)/(3)` of the job.

Now, we can write the following equation about fractions of the job done:

The fraction of the job done by the older pump plus the fraction of the job done by the newer pump in one hour should total the fraction of the job done when they work together. That is in mathematical terms:

`(1)/(9) +(1)/(x) =(1)/(3)`

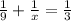
and solving for x:

`(1)/(9) +(1)/(x) =(1)/(3) \\x+9=3x\\2x=9\\x=(9)/(2) \,\,hours\\x = 4.5\,\,hours`