Answer:
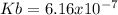
Step-by-step explanation:
Hello,
In this case, given the pH of the base, we can compute the pOH as shown below:
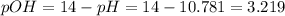
Next, we compute the concentration of the hydroxyl ions when the triethanolamine is dissociated:
![pOH=-log([OH^-])](https://img.qammunity.org/2021/formulas/chemistry/college/os6i8jhsq2yoevim3ewlj1jvyoxoba6pi1.png)
![[OH^-]=10^(-pOH)=10^(-3.219)=6.04x10^(-4)M](https://img.qammunity.org/2021/formulas/chemistry/college/21st7wn0iuef0zip08as4bvth1gb583yy2.png)
Then, by writing the equilibrium expression for the dissociation of triethanolamine we have:
![Kb=([OH^-][C6H14O2N^+])/([C6H15O3N ])](https://img.qammunity.org/2021/formulas/chemistry/college/oa0jt77qhxe1aujdgmvndpqbbqzkq7xugg.png)
That is suitable for the direct computation of Kb, knowing that based on the ICE procedure,
 equals the concentration of hydroxyl ions that was previously, computed, therefore, we have:
equals the concentration of hydroxyl ions that was previously, computed, therefore, we have:
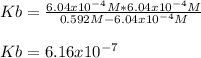
Regards.