Question

In the laboratory, a general chemistry student measured the pH of a 0.592 M aqueous solution of triethanolamine, C6H15O3N to be 10.781. Use the information she obtained to determine the Kb for this base.

Kb(experiment) =_______

Answer 1

`Kb=6.16x10^(-7)`

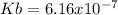
Step-by-step explanation:

Hello,

In this case, given the pH of the base, we can compute the pOH as shown below:

`pOH=14-pH=14-10.781=3.219`

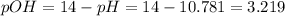
Next, we compute the concentration of the hydroxyl ions when the triethanolamine is dissociated:

`pOH=-log([OH^-])`

`[OH^-]=10^(-pOH)=10^(-3.219)=6.04x10^(-4)M`

Then, by writing the equilibrium expression for the dissociation of triethanolamine we have:

`Kb=([OH^-][C6H14O2N^+])/([C6H15O3N ])`

That is suitable for the direct computation of Kb, knowing that based on the ICE procedure,
`x` equals the concentration of hydroxyl ions that was previously, computed, therefore, we have:

`Kb=(6.04x10^(-4)M*6.04x10^(-4)M)/(0.592M-6.04x10^(-4)M)\\ \\Kb=6.16x10^(-7)`

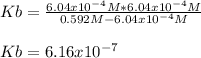
Regards.