Answer:
Calculated |t |= 7.72 > 2.1314 at 0.05 level of significance
Null hypothesis is rejected
The night shift-workers show more variability in their output levels are greater than day workers
Explanation:
Step(i):-
Given first sample size n₁ = 9
Given mean of the first sample x₁⁻ = 520
Given sample variance of the first sample'S²₁' = = 38
Standard deviation of the first sample 'S₁' = √38 =6.16
Given second sample size n₂ = 8
Given mean of the second sample x₂⁻ = 540
Given sample variance of the second sample ( 'S²₂' = 20
Standard deviation of the second sample 'S₂' = √20 = 4.4712
Step(ii):-
Null hypothesis :H₀: σ²₁ =σ²₂
Alternative Hypothesis:H₁: σ²₁ > σ²₂
Test statistic
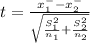
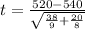
t = - 7.72
|t| = |- 7.72| = 7.72
Degrees of freedom
ν = n₁ + n₂ -2 = 9 +8 -2 = 15
t₀.₀₅ = 2.1314
Final answer:-
Calculated |t |= 7.72 > 2.1314 at 0.05 level of significance
Null hypothesis is rejected
The night shift-workers show more variability in their output levels are greater than day workers