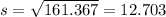Question

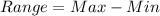
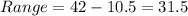
Listed below are the top 10 annual salaries​ (in millions of​ dollars) of TV personalities. Find the​ range, variance, and standard deviation for the sample data. Given that these are the top 10​ salaries, do we know anything about the variation of salaries of TV personalities in​ general?

42 40 39 31 22 18 15 12 11.7 10.5

Answer 1

`Range = Max -Min`

`Range= 42-10.5= 31.5`

The sample variance would be given by;

`s^2=(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

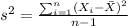
And replacing we got:

`s^2 = 161.377`

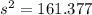
The standard deviation would be:

`s=√(161.367)=12.703`

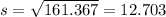
Explanation:

For this case we have the following data:

42 40 39 31 22 18 15 12 11.7 10.5

If we sort the values on increasing order we got:

10.5 11.7 12.0 15.0 18.0 22.0 31.0 39.0 40.0 42.0

The range is defined as:

`Range = Max -Min`

`Range= 42-10.5= 31.5`

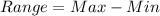
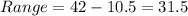
The sample variance would be given by;

`s^2=(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

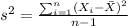
And replacing we got:

`s^2 = 161.377`

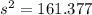
The standard deviation would be:

`s=√(161.367)=12.703`