Answer:
100
Step-by-step explanation:
Let us Assume x as the original sides of the square
As we know that
Area of rectangle is
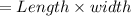
where,
Length is 12 meters
And, the width is 7 meters
Moreover, the area of the rectangle is 66 square meters
Now since the length is increased by 12 meters and the width is decreased by 7 meters
So, the equation would be
(x + 12) (x - 7) = 66
x^2 + 5x - 84 = 66
x^2 + 5x - 150 = 0
Now, we compute the factor of the above equation
(x - 10) (x + 15) = 0
We do not consider the negative root
Therefore the area of original square is
= Side^2
= 10^2
= 100