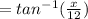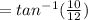Question

When x = 10 ft, the crate has a speed of 20 ft/s which is increasing at 6 ft/s^2. Determine the direction of the crate's velocity and the magnitude of the crate's acceleration at this instant.

Answer 1

The direction will be "39.8°". The further explanation is given below.

Step-by-step explanation:

The equation will be:

⇒
`y=(x^2)/(24)`

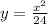
On differentiating the above, we get

⇒
`(dy)/(dx)=(2x)/(24)`

`=(x)/(12)`

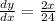
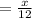
On differentiating again, we get

⇒
`(d^2y)/(dx^2)=(1)/(12)`

Demonstrate the radius of the path curvature .

⇒
`\rho=\frac{[1+((dy)/(dx))^2]^{(3)/(2)}}\left`

`=\frac{[1+((x)/(12) )^2]^{(3)/(2)}}\left`

`=\frac{[1+((10)/(12))^2]^{(3)/(2)}}{(1)/(12) }`

`=26.4 \ ft`

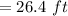
On calculating the acceleration's normal component, we get

⇒
`a_(n)=(v^2)/(\rho)`

`=(20)/(26.4)`

`=15.15 \ ft/s^2`

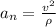
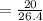
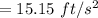
Magnitude,

⇒
`a=\sqrt{a_(n)^2+a_(t)^2}`

`=√((15.15)^2+(6)^2)`

`=16.29 \ ft/s^2`

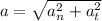
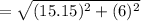
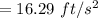
The direction of crate velocity will be:

⇒
`\phi=tan^(-1)((dy)/(dx) )`

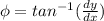
On putting the values, we get

`=tan^(-1)((x)/(12))`

`=tan^(-1)((10)/(12) )`

`=39.8^(\circ)`