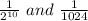Question

Which expressions are equivalent to (2 Superscript 5 Baseline) Superscript negative 2? 2–10 and StartFraction 1 Over 20 EndFraction 2–10 and StartFraction 1 Over 1024 EndFraction 10–2 and StartFraction 1 Over 100 EndFraction 10–10 and StartFraction 1 Over 100 EndFraction

Answer 1

B

Explanation:

took the pretest! good luck!

Answer 2

`(1)/(2^(10)) \ and\ (1)/(1024)`

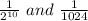
Explanation:

Given

`(2^(5))^(-2)`

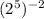
Required

Find the equivalent;

To find the equivalent of the given expression, we make use of laws of indices;

Using the following law of indices;

`(a^m)^n = a^(m*n)`

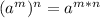
So;

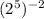`(2^(5))^(-2)` becomes

`(2^(5))^(-2) = 2^(5*-2)`

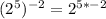
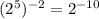`(2^(5))^(-2) = 2^(-10)` ------------ This is one equivalent

Solving further;

Using the following law of indices;

`a^(-m) = (1)/(a^m)`

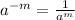
So;

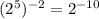`(2^(5))^(-2) = 2^(-10)` becomes

`(2^(5))^(-2) = (1)/(2^(10))`

`2^10 = 1024`

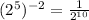
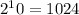
Hence;

`(2^(5))^(-2) = (1)/(1024)`

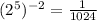
Conclusively; the equivalents of
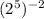`(2^(5))^(-2)` are
`(1)/(2^(10)) \ and\ (1)/(1024)`