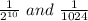Answer:
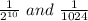
Explanation:
Given
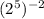
Required
Find the equivalent;
To find the equivalent of the given expression, we make use of laws of indices;
Using the following law of indices;
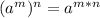
So;
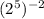 becomes
becomes
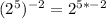
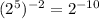 ------------ This is one equivalent
------------ This is one equivalent
Solving further;
Using the following law of indices;
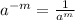
So;
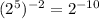 becomes
becomes


Hence;
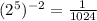
Conclusively; the equivalents of
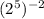 are
are