Question

the pressure p of a given gas in inversely proportional to the cube root of its volume, V at a constant temperature, When V is 64, p=6 . calculate (a) p when v=27 (d) v when f= 2​

Answer 1

see explanation

Explanation:

Given that p is inversely proportional to
`\sqrt[3]{V}` then the equation relating them is

p =
`\frac{k}{\sqrt[3]{V} }` ← k is the constant of proportion

To find k use the condition when V = 64, p = 6 , thus

6 =
`\frac{k}{\sqrt[3]{64} }` =
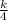`(k)/(4)` ( multiply both sides by 4 )

24 = k

p =
`\frac{24}{\sqrt[3]{V} }` ← equation of proportion

(a)

When V = 27, then

p =
`\frac{24}{\sqrt[3]{27} }` =
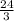`(24)/(3)` = 8

(b)

When p = 2, then

2 =
`\frac{24}{\sqrt[3]{V} }` ( multiply both sides by
`\sqrt[3]{V}` )

2
`\sqrt[3]{V}` = 24 ( divide both sides by 2 )

`\sqrt[3]{V}` = 12 ( cube both sides )

V = 12³ = 1728