Question

in 2009 a total of R36 000 was invested in two accounts. One account earned 7% annual interest and the other earned 9% .The total annual earned was R2 920 .How much was invested in each accounts?​

Answer 1

a = amount invested at 7%

b = amount invested at 9%

we know the amount invested was ₹36000, thus we know that whatever "a" and "b" are, a + b = 36000. We can also say that

`\begin{array} \cline{1-1} \textit{a\% of b}\\ \cline{1-1} \\ \left( \cfrac{a}{100} \right)\cdot b \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{7\% of a}}{\left( \cfrac{7}{100} \right)a}\implies 0.07a~\hfill \stackrel{\textit{9\% of b}}{\left( \cfrac{7}{100} \right)b}\implies 0.09b`

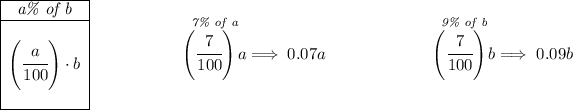
since we know the interest earned from the invested was ₹2920, then we say that 0.07a + 0.09b = 2920.

`\begin{cases} a + b = 36000\\\\ 0.07a+0.09b=2920 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{using the 1st equation}}{a + b = 36000\implies \underline{b = 36000-a}}~\hfill \stackrel{\textit{substituting on the 2nd equation}}{0.07a~~ + ~~0.09(\underline{36000-a})~~ = ~~2920} \\\\\\ 0.07a+3240-0.09a=2920\implies 3240-0.02a=2920\implies -0.02a=-320 \\\\\\ a=\cfrac{-320}{-0.02}\implies \boxed{a=16000}~\hfill \boxed{\stackrel{36000~~ - ~~16000}{20000=b}}`