Answer:
Minimum electrical power required = 3.784 Watts
Minimum battery size needed = 3.03 Amp-hr
Step-by-step explanation:
Temperature of the beverages,

Outside temperature,
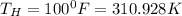
rate of insulation,
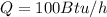
To get the minimum electrical power required, use the relation below:
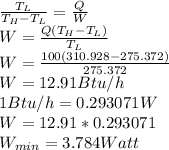
V = 5 V
Power = IV
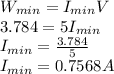
If the cooler is supposed to work for 4 hours, t = 4 hours
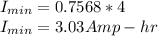
Minimum battery size needed = 3.03 Amp-hr