Answer: 9 ft, 23 ft
Explanation:
We know the Pythagorean Theorem is a²+b²=c². Since one leg is 14 less than the other leg, we can use x-14 and the other leg would be x. We can plug these into the Pythagorean Theorem with the given hypotenuse.
(x-14)²+x²=25²
(x²-28x+196)+x²=625
2x²-28x+196=625
2x²-28x-429=0
When we solve for x, we get
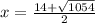 and
and
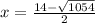 .
.
Note, since we rounded to 23, the hypotenuse isn't exactly 25, but it gets very close.