Answer:
a) From the empirical rule we know that within 3 deviations from the mean we have 99.7% of the data
b)
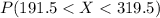
We can find the number of deviations from the mean for the limits using the z score formula given by:

And replacing we got:
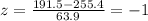
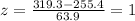
So we have values within 1 deviation from the mean and using the empirical rule we know that we have 68% of the values for this case
Explanation:
For this case we have the following properties for the random variable of interest "blood platelet counts"
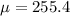 represent the mean
represent the mean
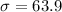 represent the population deviation
represent the population deviation
Part a
From the empirical rule we know that within 3 deviations from the mean we have 99.7% of the data
Part b
We want this probability:
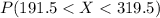
We can find the number of deviations from the mean for the limits using the z score formula given by:

And replacing we got:
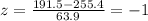
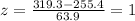
So we have values within 1 deviation from the mean and using the empirical rule we know that we have 68% of the values for this case