Question

Suppose the time it takes a barber to complete a haircuts is uniformly distributed between 8 and 22 minutes, inclusive. Let X = the time, in minutes, it takes a barber to complete a haircut. Then X ~ U (8, 22). Find the probability that a randomly selected barber needs at least 14 minutes to complete the haircut, P(x > 14) (round answer to 4 decimal places) Answer:

Answer 1

`P(X>14)= 1-P(X<14) =1- F(14)`

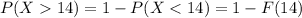
And replacing we got:

`P(X>14)= 1- (14-8)/(22-8)= 0.5714`

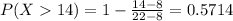
The probability that a randomly selected barber needs at least 14 minutes to complete the haircut is 0.5714

Explanation:

We define the random variable of interest as x " time it takes a barber to complete a haircuts" and we know that the distribution for X is given by:

`X \sim Unif (a= 8, b=22)`

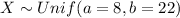
And for this case we want to find the following probability:

`P(X>14)`

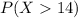
We can find this probability using the complement rule and the cumulative distribution function given by:

`P(X<x) = (x-a)/(b-a) ,a \leq x \leq b`

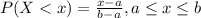
Using this formula we got:

`P(X>14)= 1-P(X<14) =1- F(14)`

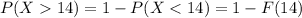
And replacing we got:

`P(X>14)= 1- (14-8)/(22-8)= 0.5714`

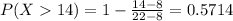
The probability that a randomly selected barber needs at least 14 minutes to complete the haircut is 0.5714