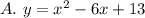Question

Which equation represents a parabola that opens upward, has a minimum at x = 3, and has a line of symmetry at x = 3?

A. y = x^2 - 6x + 13
B. y = x^2 - 8x + 19
C. y= x^2 - 3x + 6
D. y= x^2 + 6x + 5

Answer 1

A. y = x^2 -6x + 13

Explanation:

Answer 2

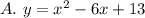`A.\ y = x^2 - 6x + 13` is the correct answer.

Explanation:

We know that vertex equation of a parabola is given as:

`y = a(x-h)^2+k`

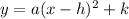
where
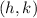`(h,k)` is the vertex of the parabola and

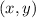`(x,y)` are the coordinate of points on parabola.

As per the question statement:

The parabola opens upwards that means coefficient of
`x^(2)` is positive.

Let
`a = +1`

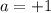
Minimum of parabola is at x = 3.

The vertex is at the minimum point of a parabola that opens upwards.

`\therefore`
`h = 3`

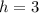
Putting value of a and h in the equation:

`y = 1(x-3)^2+k\\\Rightarrow y = (x-3)^2+k\\\Rightarrow y = x^2-6x+9+k`

Formula used:
`(a-b)^2=a^(2) +b^(2) -2* a * b`

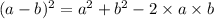
Comparing the equation formulated above with the options given we can observe that the equation formulated above is most similar to option A.

Comparing
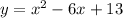`y = x^2 - 6x + 13` and
`y = x^2-6x+9+k`

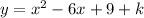
13 = 9+k

k = 4

Please refer to the graph attached.

Hence, correct option is
`A.\ y = x^2 - 6x + 13`