Question

The water from a fire hose follows a path described by y equals 2.0 plus 0.9 x minus 0.10 x squared ​(units are in​ meters). If v Subscript x is constant at 10.0 ​m/s, find the resultant velocity at the point left parenthesis 9.0 comma 2.0 right parenthesis .

Answer 1

The resultant velocity is 12.21 m/s.

Explanation:

We are given that the water from a fire hose follows a path described by y equals 2.0 plus 0.9 x minus 0.10 x squared ​(units are in​ meters).

Also, v Subscript x is constant at 10.0 ​m/s.

The water from a fire hose follows a path described by the following equation below;

`y=2.0 + 0.9x-0.10x^(2)`

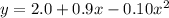
The velocity of the
`x` component is constant at =
`v_x=10.0 \text{ m/s}`

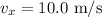
and the point at which resultant velocity has to be calculated is (9.0,2.0).

Let the velocity of x and y component be represented as;

`v_x=(dx)/(dt) \text{ and } v_y=(dy)/(dt)`

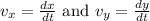
Now, differentiating the above equation with respect to t, we get;

`y=2.0 + 0.9x-0.10x^(2)`

`(dy)/(dt) =0 + 0.9(dx)/(dt) -(0.10* 2)(dx)/(dt)`

`(dy)/(dt) = 0.9(dx)/(dt) -0.2(dx)/(dt)`

`v_y = 0.9v_x -0.2v_x`

`v_y = 0.7v_x`

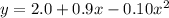
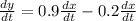
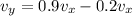
Now, putting
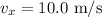`v_x=10.0 \text{ m/s}` in the above equation;

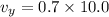`v_y = 0.7 * 10.0` = 7 m/s

Now, the resultant velocity is given by =
`v=\sqrt{v_x^(2)+v_y^(2) }`

`v=\sqrt{10^(2)+7^(2) }`

=
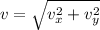
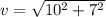
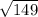`√(149)` = 12.21 m/s