Question

A specimen of a 4340 steel alloy with a plane strain fracture toughness of 54.8 MPa (50 ksi ) is exposed to a stress of 2023 MPa (293400 psi). Assume that the parameter Y has a value of 1.14. (a) If the largest surface crack is 0.2 mm (0.007874 in.) long, determine the critical stress .

Answer 1

Step-by-step explanation:

The formula for critical stress is

`\sigma_c=(K)/(Y√(\pi a) )`

`\sigma_c =\texttt{critical stress}`

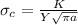
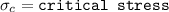
K is the plane strain fracture toughness

Y is dimensionless parameters

We are to Determine the Critical stress

Now replacing the critical stress with 54.8

a with 0.2mm = 0.2 x 10⁻³

Y with 1

`\sigma_c=\frac{54.8}{1\sqrt{\pi * 0.2*10^(-3)} } \\\\=\frac{54.8}{\sqrt{6.283*10^(-4)} } \\\\=(54.8)/(0.025) \\\\=2186.20Mpa`

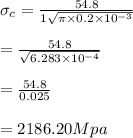
The fracture will not occur because this material can handle a stress of 2186.20Mpa before fracture. it is obvious that is greater than 2023Mpa

Therefore, the specimen does not failure for surface crack of 0.2mm