Question

Joey is building a frame for a sandbox. The sandbox is going be have the shape and dimensions below. If the diagonal of the sandbox measures 14 feet, what kind of quadrilateral will the sandbox be? Explain how you know.

Answer 1

Quadrilateral

Explanation:

In the sandbox, opposite sides are equal.

However, using Pythagoras Theorem

`14^2\\eq 12^2+8^2\\196 \\eq 208`

Therefore, the sandbox cannot be a rectangle since if it were, each triangle must be a right triangle.

In the triangle

• If
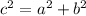  `c^2=a^2+b^2`, C is a right angle
• If
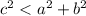  `c^2<a^2+b^2`, C is an acute angle
• If
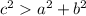  `c^2>a^2+b^2` , C is an obtuse angle

Since
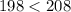`198<208`, Angles C and X are acute angles.

Therefore, the sandbox does not satisfy the properties of any known quadrilateral. It is simply a quadrilateral-shaped sandbox.