Answer:
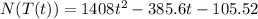
Time for bacteria count reaching 8019: t = 2.543 hours
Explanation:
To find the composite function N(T(t)), we just need to use the value of T(t) for each T in the function N(T). So we have that:
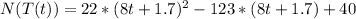
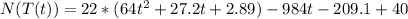
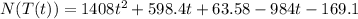
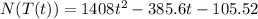
Now, to find the time when the bacteria count reaches 8019, we just need to use N(T(t)) = 8019 and then find the value of t:
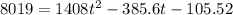
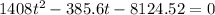
Solving this quadratic equation, we have that t = 2.543 hours, so that is the time needed to the bacteria count reaching 8019.