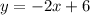Question

The points A(-3, 2) and B(1,4) are vertices of an isosceles triangle ABC, where angle B = 90°

(0) Find the length of the line AB.

(ii) Find the equation of the line BC.

Answer 1

Length of AB = 4.4721

Equation of line BC: y = -2x + 6

Explanation:

To find the length of the line AB, we just need to find the distance between the points A and B.

We can find distance with the equation:

`distance = √((x_A - x_B)^2 + (y_A - y_B)^2)`

`distance = √((-3 - 1)^2 + (2 - 4)^2)`

`distance = 4.4721`

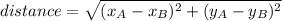
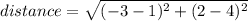
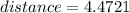
To find the equation of the line BC, first let's find the slope of the line AB.

This slope is given by:

`m_(AB) = ( y_A - y_B )/( x_A - x_B )`

`m_(AB) = ( 2 - 4 )/( -3 - 1) = (1)/(2)`

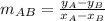
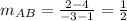
The line AB is perpendicular to the line BC (because mB = 90°), so the slope of line BC is:

`m_(BC) = -(1)/(m_(AB)) = -2`

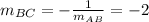
so the line BC is:

`y = -2x + b`

To find the value of b, we can use the point B (1,4):

`4 = -2 + b`

`b = 6`

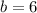
So we have:

`y = -2x + 6`