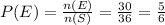Question

Two fair six-sided dice are rolled. What is the probability that the product of the two numbers is a composite number? Express your answer as a common fraction.

Answer 1

29/36

Explanation:

AoPs Answer

Answer 2

The probability that the product of the two numbers is a composite number

`P(E) = (5)/(6)`

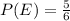
Explanation:

Step(i):-

Given data Two fair six-sided dice are rolled

S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6) ,(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),((4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}

The number of exhaustive cases

n(S) =36

Composite number :-

A composite number has more than two factors

Example :-

Find composite numbers 1 to 10

{ 4, 6, 8.9,10}

Step(ii):-

Let 'E' be the event of getting the product of the two numbers is a composite number

= {(1,4),(1,5),(1,6),(2,2),(2,3),(2,4),(2,5),(2,6),(3,2),(3,3),(3,4),(3,5),(3,6),((4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}

n(E) = 30

Conclusion:-

The probability that the product of the two numbers is a composite number

`P(E) = (n(E))/(n(S)) = (30)/(36) = (5)/(6)`