Answer:
Total momentum before collision = 16 × 10³ kg.m/s
Total momentum after collision = 16,000 kg.m/s
Velocity after collision = 0.696 m/s
total Kinetic energy before collision = 16,000 J
Total Kinetic energy after collision = 5,600 J
Step-by-step explanation:
This Kind of collision is called perfectly Inelastic Collision, because both objects stick together, and move in the same direction after collision.
Using the principle of conservation of momentum, which states that in a system, total momentum before collision is the same as total momentum after collision, the Net momentum of the system can be written as:
momentum before collision = momentum after collision
M₁V₁ + M₂V₂ = (M₁ + M₂)Vₓ
where:
M₁ = Mass of locomotive = 8,000 kg
V₁ = speed of locomotive = 2.0 m/s
M₂ = Mass of car = 15,000 kg
V₂ = speed of car = 0 m/s (stationary car)
Vₓ = final velocity after collision
The total momentum before collision = M₁V₁ + M₂V₂
(8,000 × 2) + (15,000 × 0) = 16,000 + 0 = 16,000 kg.m/s
∴ The total momentum before collision = 16,000 kg.m/s = 16 × 10³ kg.m/s
since Total momentum is conserved, momentum after collision = 16,000 kg.m/s
Finding velocity after collision
M₁V₁ + M₂V₂ = (M₁ + M₂)Vₓ
= (8,000 × 2) + (15,000 × 0) = (8,000 + 15,000) Vₓ
16000 + 0 = (23,000)Vₓ
23,000Vₓ = 16,000
∴ Vₓ = 16,000 ÷ 23,000 = 0.696 m/s
Velocity after collision = 0.696 m/s
Finally the total Kinetic energy before collision =
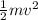
=
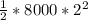
= 4000 × 4 = 16,000 J
∴ Finally the total Kinetic energy before collision = 16,000 J
Total Kinetic energy after collision =
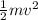
=
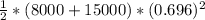
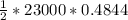
= 11,500 × 0.4844 = 5570.6 ≈ 5,600 Joules