Answer:
The approximated length of the cables that stretch between the tops of the two towers is 1245.25 meters.
Explanation:
The equation of the parabola is:
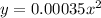
Compute the first order derivative of y as follows:
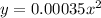
![\frac{\text{d}y}{\text{dx}}=\frac{\text{d}}{\text{dx}}[0.00035x^(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/8qmtip8n4uwcy7b5f5k2pk9nyslaj4k4b1.png)
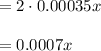
Now, it is provided that |x | ≤ 605.
⇒ -605 ≤ x ≤ 605
Compute the arc length as follows:
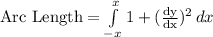
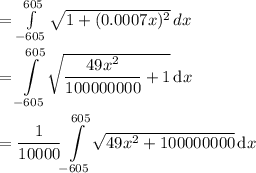
Now, let

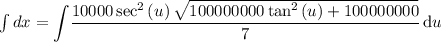
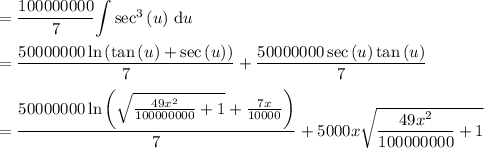
Plug in the solved integrals in Arc Length and solve as follows:
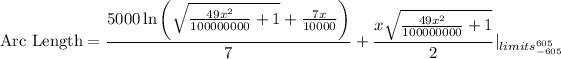
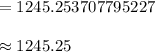
Thus, the approximated length of the cables that stretch between the tops of the two towers is 1245.25 meters.