Question

A diameter shaft contains a deep U-shaped groove that has a radius at the bottom of the groove. The maximum shear stress in the shaft must be limited to . If the shaft rotates at a constant angular speed of , determine the maximum power that may be delivered by the shaft.

Answer 1

hello your question lacks the required figures here is the complete question

A 1.25-in diameter shaft contains a 0.25-in deep U-shaped groove that has a 1/8-in radius at the bottom of the groove. The maximum shear stress in the shaft must be limited to 12000 psi . If the shaft rotates at a constant angular speed of 6Hz , determine the maximum power that may be delivered by the shaft.

Answer: max power delivered by shaft = 4.045 hp

Step-by-step explanation:

Determine The maximum power that can be delivered by the shaft

using the given data

diameter of shaft ( D ) = 1.25 inches

depth of U-shaped groove = 0.25 inches

radius of U-shaped groove = 1/8 inches = 0.125 inches

maximum shear stress in shaft = 12000 psi

shaft angular speed at frequency of 6 Hz

firstly calculate

The minor diameter (d) = 1.25 - 2(0.25 ) = 0.5 inches

Ratio = radius of groove / minor diameter = 0.125 / 0.75 = 0.167

Ratio, = diameter of shaft / minor diameter = 1.25 / 0.75 = 1.667

k = 1.39 from stress concentration factors graph

calculate the maximum shear stress produced by the torque in the minor diameter of the shaft

Tmax =
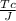`(Tc)/(J)` -----------equation 1

where Tc = 16T

J =
`\pi d^(3)`

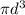
equation 1 becomes( Tmax ) =
`(16*T)/(\pi *0.75^3)`

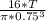
also Tmax = K * Tmin -------- equation 2

1.39 *
`(16*T)/(\pi *0.75^3 ) \leq 1200`

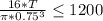
T ≤ 715.122 Ib-in

Tmax = 59.593 Ib-ft ( max shear stress )

Finally calculate the max power transmitted by the shaft

P max = 2
`\pi`fTmax = 2
`\pi` * 6 * 59.593

therefore Pmax = 2246.6 Ib-ft/s

= 4.045 hp